最近重新拾起 Sedgewick 的《算法（第4版）》，对之前学的不扎实的算法和数据结构做个回顾。红黑树的实现和删除比较复杂，这里对书中一些描述不够清晰甚至有疏漏的地方进行注解。术语的表述基本与《算法》一致，避免使用乱七八糟的『亲戚称呼』。

红黑树的难点在于『写操作』，即put和delete方法的实现。这里以put方法的实现和简单分析作为热身，着重讨论书中描述不够清晰的delete方法的实现。全面的讲解请看原著和普林斯顿大学的授课PPT，此外有完整代码和完整论文。

2-3树和红黑树

由于红黑树（LLRB Tree）可以看做是用二叉搜索树（BST）实现的2-3树，所以从2-3树入手，讨论过程中随时回到2-3树进行比对分析。

2-3树为什么能保持完美平衡？

直观的说，插入时，总是通过『膨胀』使得原键的『度』增加，再做『适当调整』使得树保持平衡并满足2-3树的基本性质（左倾、只有2-结点和3-结点）；当出现4-结点时，『调整操作』会使得树长高，因为总是『提出』4-结点中的『中间键』，所以能保持完美平衡。

对于红黑树，我们可以这么理解，

红链接沿着『中间结点』向上传递。

插入操作

第一轮热身： 红黑树插入操作的实现，基于BST的插入操作，关键在于实现上述的『膨胀』、『适当调整』和『提出中间键』，即『新插入结点染为红色』、用『左旋』保证左倾、『右旋』和『反色』保证中间结点上移。

以上状态转移图描述了所有需要考虑的情形，可以得出三种调整的先后顺序。插入操作代码如下，注释部分为红黑树有别于BST的代码：

    public void put(Key key, Value value) {
        root = put(root, key, value);
        //根节点链接为黑色
        root.color = BLACK;
    }

    private Node put(Node node, Key key, Value value) {
        if (node == null)   // 新建结点为红色
            return new Node(key, value, 1, RED);

        int cmp = key.compareTo(node.key);
        if (cmp < 0)       node.left = put(node.left, key, value);
        else if (cmp > 0)  node.right = put(node.right, key, value);
        else               node.value = value;

        //『左旋』保证左倾
        if (!isRed(node.left) && isRed(node.right)) node = rotateLeft(node);
        //『右旋』和『反色』保证中间结点上移
        if (isRed(node.left) && isRed(node.left.left)) node = rotateRight(node);
        if (isRed(node.left) && isRed(node.right)) flipColors(node);

        node.N = size(node.left) + size(node.right) + 1;
        return node;
    }

上述插入代码在递归向下过程中不断搜索直到找到『合适位置』将新结点插入，回溯过程中对树进行『修正操作』。

如果我们将上述代码中的if (isRed(node.left) && isRed(node.right)) flipColors(node);这句提前到递归前（比较操作之前），即把递归向上时的最后一步『反色』操作，『延迟』到下次插入操作之前，这样插入完成后树中将存在4-结点，生成的是2-3-4树。

删除最大最小键

第二轮热身： 删除最小键和最大键。在2-3树中，删除底部的2-结点会影响树的完美平衡，而删除3-结点或4-结点中的键则没有问题。

删除操作可以视为插入操作的『逆操作』。如删除最小键操作中，沿着左链接向下变换使得红链接向左下移动，确保当前结点不是2-结点。

以删除最小键为例展开说明：

• 如果当前结点的左子结点不是2-结点，不处理；
• 如果当前结点的左子结点是2-结点，且左子结点的『亲兄弟』结点也是2-结点，将当前结点的最小键、左子结点和其『亲兄弟』结点三个键合并成一个4-结点；
• 如果当前结点的左子结点是2-结点，且左子的『亲兄弟』结点是3-结点，向其『亲兄弟』结点『借』一个键，使得左子结点成为3-结点；

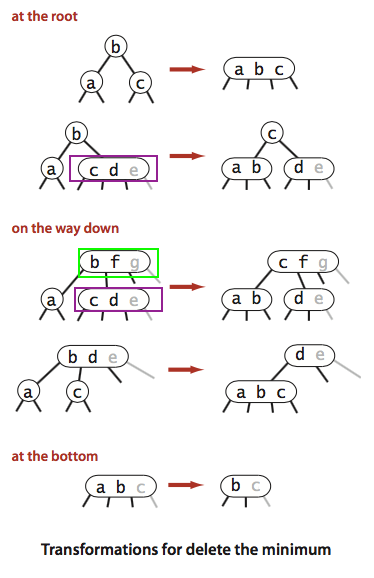
下图是《算法》书上2-3树删除最小键过程中所进行的变换。

这张图有点问题： 我们在向下变换过程中，只允许当前结点及『所过结点』出现临时的4-结点（绿色矩形标识），当前结点的右子结点是不可能出现4-结点的（紫色矩形标识），这些临时4-结点或被接下来的变换拆散，或在向上回溯过程中被修复。我在上述第三点说明时将原书的『不是2-结点』改为了『3-结点』也是出于此。

对于根节点需要留意下，在实际红黑树操作中如果根节点的左右结点都是黑链接，我们把指向根节点的链接『假装』成红色，也就是假装根节点的键在3-结点中。

回到红黑树似乎看起来更清晰，current.right.left的颜色决定了是否要向兄弟结点借：

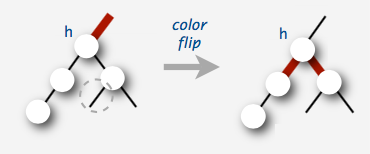
上述第二种情形，仅需要进行颜色反转操作：

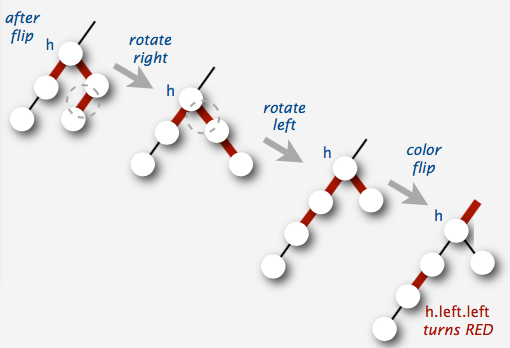
上述第三种情形，向兄弟结点借：

代码也很简洁：

    public void deleteMin() {
        if (!isRed(root.left) && !isRed(root.right))
            root.color = RED;
        root = deleteMin(root);
        if (!isEmpty())
            root.color = BLACK;
    }

    private Node deleteMin(Node node) {
        if (node.left == null)
            return null;
        if (!isRed(node.left) && !isRed(node.right))
            node = moveRedLeft(node);
        node = deleteMin(node);
        return fixUp(node);
    }

    private Node moveRedLeft(Node node) {
        flipColors(node);
        if (isRed(node.right.left)){
            node.right = rotateRight(node.right);
            node = rotateLeft(node);
            flipColors(node);
        }
        return node;
    }
    
    private Node fixUp(Node node) {
        if (isRed(node.right)) node = rotateLeft(node);
        if (isRed(node.left) && isRed(node.left.left)) node = rotateRight(node);
        if (isRed(node.left) && isRed(node.right)) flipColors(node);
        return node;
    }

这里的fixUp即向上回溯过程中的『修复』操作，与插入操作中回溯时的代码几乎一样。第一个判断改成了if (isRed(node.right))而不是if (!isRed(node.left) && isRed(node.right))（Why？）。

对于删除最大键，由于树是左倾的，稍有不同，直接看代码画图分析即可：

    private Node deleteMax(Node node) {
        if (isRed(node.left))
            node = rotateRight(node);
        if (node.right == null)
            return null;
        if (!isRed(node.right) && !isRed(node.right.left))
            node = moveRedRight(node);
        return fixUp(node);
    }

    private Node moveRedRight(Node node) {
        flipColors(node);
        if (isRed(node.left.left)) {
            node = rotateRight(node);
            flipColors(node);
        }
        return node;
    }

删除任意键

总是删除最底部的键。当遇到待删除的结点时，使用右子树中的最小结点替换待删除结点。向左搜索时，使用moveRedLeft，向右搜索时使用moveRedRight。

代码结合了deleteMin和deleteMax，其中①处表示待删除的结点正好在底部，可以直接删除，②处使用了小技巧，使用右子树的最小结点的key和val更新待删除结点的属性。和之前一样，需要在回溯过程中修复红黑树。

    private Node delete(Node node, Key key) {
        int cmp = key.compareTo(node.key);
        if (cmp < 0){
            if (!isRed(node.left) && isRed(node.left.left))
                node = moveRedLeft(node);
            node.left = delete(node.left, key);
        } else {
            if (isRed(node.left))
                node = rotateRight(node);
            if (cmp == 0 && node.right == null) // ①
                return null;
            if (!isRed(node.right) && !isRed(node.right.left))
                node = moveRedRight(node);
            if (cmp == 0) {                     // ②
                node.value = get(node.right, min(node.right).key);
                node.key = min(node.right).key;
                node.right = deleteMin(node.right);
            }
            else node.right = delete(node.right, key);
        }
        return fixUp(node);
    }

小结： 红黑树的删除操作实现起来确实很难也很繁琐，结合2-3树并使用LLRB能够降低一部分难度。然而还是有些细节值得推敲琢磨。