Generative Adversarial Networks (GANs, 生成对抗网络) 是一种由两个网络构成的通过对抗学习训练的生成模型，由 Ian Goodfellow 等人（包括 Yoshua Bengio）在 2014 年提出，并得到了 Yann LeCun 的盛赞，称其为『机器学习界10年来最有趣的点子』。

本文将从新手的角度介绍GAN的思想和实现方法，前置知识仅需要神经网络基础。

监督 vs. 非监督

几乎所有人学习神经网络都是从分类器学起的，也就是『喂给』神经网络的数据集包括两部分：原始数据（x）和标注（y），我们希望构造一个复杂的非线性函数来表示 $f:x \rightarrow y$ 的映射，这是监督学习，如分类、回归、目标检测、语义分割等。

对于非监督学习，训练数据仅有原始的数据而没有标记，我们希望算法学习数据中隐含的模式或结构，如聚类，降维，特征学习等。

本文所述的 GAN，也是最简单最原始的GAN，是非监督学习，我知道对于大部分新手来说用神经网络做非监督学习是不太好接受的。

生成算法 vs. 分类算法

GAN 作为一种生成算法，其目标是能够『模仿』给定数据集中的数据，生成新的符合数据集特征的数据。

我们先来回忆简单的二分类算法。例如，对于一个垃圾邮件分类（鉴别）算法，给定邮件内容中的所有文本，分类器能够预测出该文本是否是垃圾。用一个简单的数学表达式表示即为 $P(y|x)$，其中$x$为输入分类器的特征，$y$为标签，分类器能够预测给定的$x$类别为$y$的概率。也就是分类器是从高维特征向低维标签的映射。

生成算法的目标与分类算法的目标正好相反，生成器试图从给定的低维标签生成高维的特征，即试图得到 $P(x|y)$。

也就是说，将简单的分类网络前后翻转，就是一个生成网络了。问题在于，如何训练这个生成网络，使其能够模仿训练集来生成数据，或者说学习到训练集中的数据分布。

GAN 的结构

GAN 是由两个神经网络，即生成器（Generator）和鉴别器（Discriminator）构成的。

所谓鉴别器，就是一个简单的二分类神经网络，或者叫分类器，用于判定输入的图片是来自于真实的数据集还是由生成器生成的。以下代码用Keras实现一个二分类的全连接网络，即为鉴别器。

# Disctiminator
D = Sequential([
    Flatten(input_shape=img_shape, name='flatten'),
    Dense(512, activation='relu', name='fully_connected1'),
    Dense(256, activation='relu', name='fully_connected2'),
    Dense(1, activation='sigmoid', name='classifier')
])

生成器网络将输入的低维度向量（这里用长度100的向量）映射到一个高维度向量后reshape到图片尺寸。Keras 实现如下。

# Generator
G = Sequential([
    Dense(256, activation='relu', input_dim=latent_dim, name='fully_connected1'),
    Dense(512, activation='relu', name='fully_connected2'),
    Dense(1024, activation='relu', name='fully_connected3'),
    Dense(np.prod(img_shape), activation='tanh', name='output_generated'),
    Reshape(img_shape)
])

当我们用训练好的神经网络生成数据时，鉴别器D就没有用了，只需要一行代码即可让生成器G生成一张图片 img = G.predict(noise_vector)。也就是说，鉴别器D对于GAN来说只是用来『帮助』训练生成器G的参数的。

虽然网络结构很简单，但如何让生成器生成满意的图像，或者说让生成器学习到训练集的数据分布才是GAN的核心。

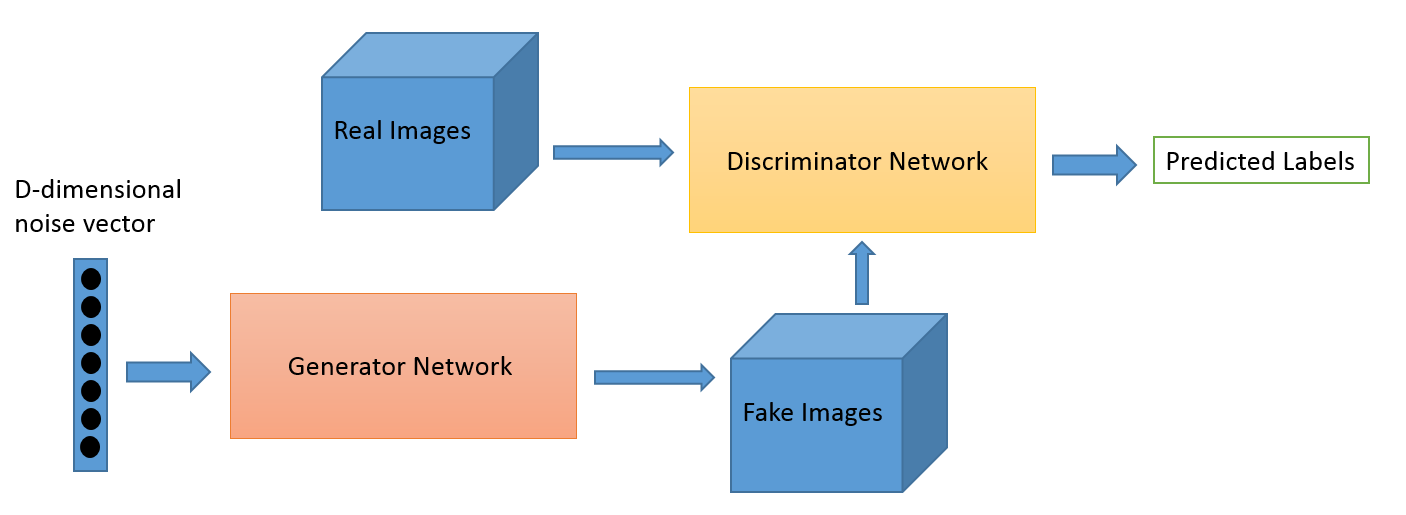
对抗训练

我们有了生成器G和鉴别器D，需要将其组合在一起训练，即为对抗训练（Adversarial Training）。所谓对抗训练，就是在参数学习过程中鉴别器D和生成器G朝着对立的方向学习：D试图不断提高分别图片真假的能力，G试图不断生成更逼真的图片来糊弄D。

GAN 训练的过程如下：

• 训练D：G接收一个随机向量作为输入，输出一张图像，用生成的图像作为负样本（label为假），训练集中的图像作为正样本训练D（label为真）
• 训练G：G再生成一张图像作为正样本（label为真）输入D，经由D的代价函数后反向传播，更新G的参数（此时D的参数锁定）

我将这个过程总结为：分别训练，共同进步。在每一步中，D和G的参数分别更新；在整个训练过程中，D和G同步提高。

用Keras实现的对抗训练代码如下。

# 编译D
D.compile(loss='binary_crossentropy', optimizer=d_optimizer, metrics=['accuracy'])
# 将D和G"串联"，得到模型C
z = Input(shape=(latent_dim,))
generated_img = G(z)
D.trainable = False       # 模型C中D的参数锁定
validity = D(generated_img)
# Combined model
C = Model(z, validity)
C.compile(loss='binary_crossentropy', optimizer=g_optimizer)
C.summary()

# load data
(x_train, _), (_, _) = mnist.load_data()
x_train = x_train / 127.5 - 1
# (60000, 28, 28) -> (60000, 28, 28, 1)
x_train = np.expand_dims(x_train, axis=3)
valid = np.ones((batch_size, 1))
fake = np.zeros((batch_size, 1))

for epoch in range(epochs):
    for _ in range(x_train.shape[0] // batch_size):
        # train D
        idx = np.random.randint(low=0, high=x_train.shape[0], size=batch_size)
        imgs = x_train[idx]
        noise = np.random.normal(0, 1, (batch_size, latent_dim))
        gen_imgs = G.predict(noise)
        D.train_on_batch(imgs, valid)
        D.train_on_batch(gen_imgs, fake)
        # train G
        noise = np.random.normal(0, 1, (batch_size, latent_dim))
        C.train_on_batch(noise, valid)

看完代码，相信你心中的诸多疑惑已经解开。

小结

本文试图抛开公式和理论，以直观的方式来介绍GAN的结构与对抗训练过程，并强调在实现过程中理解和掌握GAN。GAN 首先是一种无监督学习和生成算法，其核心思想在于对抗训练。至于公式和理论分析，我相信这时候去阅读原论文会是个不错的选择。